The 5 Best How To Calculate Area Under Curve Calculators of 2025 (R…
Finding the Best How To Calculate Area Under Curve: An Introduction
Finding the area under a curve is a fundamental concept in calculus with numerous applications in fields such as physics, economics, and statistics. However, for many, the challenge lies in identifying a reliable and user-friendly tool to perform this calculation accurately. With a plethora of online calculators and resources available, it can be overwhelming to sift through options that vary in functionality, ease of use, and reliability.
This article aims to simplify your search by reviewing and ranking the top online tools designed for calculating the area under a curve. We understand that not all tools are created equal, and our goal is to save you time by providing a curated list of the best options available. Whether you are a student needing quick calculations for homework, a professional seeking precise data for analysis, or someone interested in understanding the concept better, we’ve got you covered.
To ensure our rankings are objective and helpful, we evaluated each tool based on several key criteria. Accuracy is paramount; we assessed how well each tool performs the calculations compared to standard methods. Ease of use is another critical factor, as an intuitive interface can greatly enhance the user experience, especially for those new to the concept. Lastly, we considered the features each tool offers, such as support for different types of curves, integration methods, and the ability to visualize results.
By the end of this article, you will have a clear understanding of the best tools available to calculate the area under a curve, helping you make an informed choice tailored to your needs.
Our Criteria: How We Selected the Top Tools
When selecting the best online tools for calculating the area under a curve, we considered several important criteria to ensure that users receive accurate, reliable, and user-friendly options. Below is a detailed breakdown of the key factors we evaluated:
1. Accuracy and Reliability
- Precision of Calculations: The primary function of these tools is to provide accurate area calculations. We prioritized tools that are based on solid mathematical principles and have been validated through multiple use cases.
- User Feedback: We reviewed user testimonials and expert opinions to gauge the reliability of each tool in providing correct results consistently.
2. Ease of Use
- User Interface: An intuitive and clear interface is crucial. Tools that are cluttered or overly complex can deter users, especially those who may not be familiar with advanced mathematical concepts.
- Accessibility: We looked for tools that are accessible on various devices (desktop, tablet, mobile) and do not require extensive prior knowledge to operate effectively.
3. Key Features
- Input Flexibility: The ability to input various types of equations (polynomials, trigonometric functions, etc.) is essential. We evaluated tools that allow users to enter equations in standard formats, as well as those that can handle multiple equations for area calculations between curves.
- Boundary Specification: A good tool should enable users to easily set upper and lower limits for integration, which is fundamental for calculating the area under a curve.
- Graphical Representation: Tools that provide visual representations of the curves and shaded areas can enhance understanding and make it easier for users to verify their inputs and outputs.
4. Cost (Free vs. Paid)
- Cost-Effectiveness: We assessed whether the tools are free or if they require a subscription or one-time payment. Free tools with robust features were given preference, but we also considered paid options that offer superior functionality and support.
- Trial Periods: Some paid tools offer trial periods that allow users to test their features without commitment. We included tools that provide such options, as they allow users to evaluate their suitability.
5. Support and Documentation
- Help Resources: Comprehensive documentation, including tutorials, FAQs, and user guides, is vital for users who may need assistance. We looked for tools that offer extensive help resources to facilitate user understanding and troubleshooting.
- Customer Support: Availability of customer support through chat, email, or forums was also considered, as this can greatly enhance the user experience.
6. Additional Functionalities
- Integration with Other Tools: We examined whether the calculators could integrate with other educational tools or platforms, which can be beneficial for students and educators alike.
- Advanced Options: Features such as step-by-step solutions, historical data analysis, or the ability to export results in various formats were also considered valuable enhancements.
By evaluating these criteria, we aimed to provide a comprehensive list of the best online tools for calculating the area under a curve, ensuring that users can find the solution that best fits their needs and skill levels.
The Best How To Calculate Area Under Curves of 2025
3. Finding the Area Under the Curve in Calculus
The wikiHow article on “Finding the Area Under the Curve in Calculus” provides a straightforward guide to calculating the area beneath a curve using definite integrals. It emphasizes the essential formula \( A = \int_{a}^{b} f(x) \, dx \), which serves as the foundation for this mathematical process. The article is designed to help learners understand the concept of definite integrals and apply it effectively to solve problems related to areas under curves.
- Website: wikihow.com
- Established: Approx. 21 years (domain registered in 2004)
4. Fastest way to find the area under a curve which is represented by a …
The discussed method provides a quick approach to calculate the area under a curve represented by discrete data points. By averaging the y-values of evenly spaced x-values and multiplying the result by the spacing between x-values and one less than the total number of points, users can efficiently estimate the area. This technique is particularly useful for data sets with uniform intervals, streamlining the process of integration.
- Website: math.stackexchange.com
- Established: Approx. 16 years (domain registered in 2009)
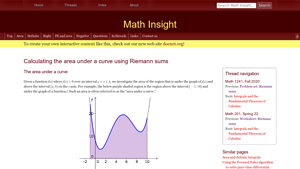
5. Calculating the area under a curve using Riemann sums
The “Calculating the Area Under a Curve Using Riemann Sums” tool on Math Insight serves to approximate the area beneath a positive function’s graph by summing the areas of rectangles. This educational resource effectively illustrates the concept of Riemann sums, enabling users to visualize and understand the approximation process. Its clear explanations and interactive features make it a valuable tool for students and educators looking to grasp integral calculus fundamentals.
- Website: mathinsight.org
- Established: Approx. 16 years (domain registered in 2009)
How to Get the Most Accurate Results
Double-Check Your Inputs
One of the most common reasons for inaccurate results when calculating the area under a curve is incorrect input data. Always take a moment to verify that you’ve entered the correct equation of the curve, boundary limits, and any other parameters required by the calculator. A simple typo or wrong boundary can drastically alter the outcome.
Understand the Underlying Assumptions
Different online tools may utilize various methods for calculating the area under a curve, such as numerical integration, trapezoidal rule, or Simpson’s rule. Each method has its assumptions and limitations. Familiarize yourself with how the tool you are using processes the data to better interpret the results. For instance, some calculators may assume continuous functions, while others might work with discrete data points. Understanding these assumptions will help you gauge the reliability of the results.
Use Multiple Tools for Comparison
To ensure accuracy, it’s wise to use more than one online calculator for your area-under-curve calculations. By comparing results from different tools, you can identify discrepancies and better understand the range of possible answers. If one tool provides a significantly different result from the others, it may warrant further investigation into the inputs or the methodology used by that particular calculator.
Review the Output
Once you receive the results from an online calculator, take a moment to review the output critically. Consider whether the value makes sense within the context of your problem. For example, if you’re calculating the area under a curve that should yield a positive value and the result is negative, it indicates a potential error in your inputs or the calculator’s processing.
Consult Additional Resources
If you’re new to calculating areas under curves, it can be beneficial to consult additional resources, such as tutorials or instructional videos. These resources can provide you with a clearer understanding of the concepts behind the calculations and may offer insights into common pitfalls. Familiarizing yourself with the mathematical principles involved can help you use online tools more effectively.
Seek Help When Needed
If you encounter difficulties in obtaining accurate results, don’t hesitate to seek help. Online forums, math tutoring services, or academic resources can provide guidance. Engaging with a community of learners or experts can clarify complex topics and enhance your understanding of the area under the curve calculations.
By following these tips, you can maximize the accuracy and reliability of the results obtained from online calculators for calculating the area under curves.
Frequently Asked Questions (FAQs)
1. How can I find the area under a curve?
To find the area under a curve, you can use the process of integration. You need to know the equation of the curve (y = f(x)), the limits of integration (the points along the x-axis that define the area), and the axis that bounds the area. The formula used for calculating the area is:
[ A = \int_a^b f(x) \, dx ]
where ( a ) and ( b ) are the lower and upper limits, respectively.
2. What methods can I use to calculate the area under a curve?
There are several methods to calculate the area under a curve:
-
Rectangular Approximation: This method involves breaking the area under the curve into small rectangles and summing their areas. You can use either the left endpoints, right endpoints, or midpoints of each rectangle to approximate the area.
-
Trapezoidal Rule: This method approximates the area by dividing it into trapezoids instead of rectangles, providing a more accurate estimate.
-
Integration: The most precise method involves using calculus to find the integral of the function that defines the curve between the specified limits.
3. What does the area under the curve represent?
The area under the curve represents the accumulated value of the function over a specified interval. For example, in a velocity-time graph, the area under the curve indicates the total distance traveled during that time period. In general, it can represent various quantities depending on the context, such as probability, total cost, or total revenue in economics.
4. Can I calculate the area under a curve without using integration?
Yes, you can estimate the area under a curve without using integration by employing numerical methods such as the rectangular approximation or trapezoidal rule. These methods involve dividing the area into smaller shapes (rectangles or trapezoids) and calculating their areas to obtain an overall estimate.
5. When is the area under the curve negative, and how is it interpreted?
The area under the curve is considered negative when the curve lies below the x-axis. In such cases, the area can still be calculated using the same integration techniques, but the result will be a negative value. To interpret this in practical terms, you can take the absolute value of the area to represent the magnitude, as the negative sign indicates the position of the curve relative to the x-axis rather than the physical area itself.
Important Disclaimer
⚠️ Important Disclaimer
The information and reviews in this guide are for educational purposes only and are based on publicly available information. We are not affiliated with any of the tools mentioned. Features and pricing may change. Always conduct your own research before choosing a tool for your needs.